Python is renowned for its versatility and simplicity, allowing developers to perform complex mathematical operations with ease. Among the powerful mathematical concepts it supports, exponents hold a special place. In this guide, we’ll delve into the world of exponents in Python, from the basics of exponentiation to advanced applications.
Introduction to Exponents
Exponents are a fundamental mathematical concept that represents repeated multiplication of a base number by itself. In Python, you express exponents using the ** operator. For example, 2 ** 3 calculates 2 raised to the power of 3, resulting in 8.
Understanding the Basics
Exponents consist of two main components: the base and the exponent. The base is the number being raised, while the exponent signifies how many times the base is multiplied by itself.
Exponential Calculations Made Easy
Python simplifies complex exponential calculations. For instance, computing large numbers like 10^20 is as simple as 10 ** 20. Python’s flexibility extends to fractional exponents as well.
Exponents and Functions
Exponential functions are vital in various scientific and financial applications. Python’s math module provides access to essential functions.
The math.pow() Function
Python’s math module includes the pow() function, enabling accurate exponentiation. This function takes two arguments: the base and the exponent.
The math.exp() Function
The exp() function in Python returns the exponential value of a given number. It’s commonly used in calculus and statistics.
Exponents in Data Science
Exponents play a crucial role in data science and analysis.
Exponential Growth and Decay
Exponential growth and decay are prevalent in fields like biology, economics, and physics. Python facilitates modeling such phenomena.
Compounding Interest Calculations
The financial sector benefits from exponentials in calculating compound interest. Python assists in creating precise financial models.
Advanced Concepts in Exponents
Delve deeper into exponents with these advanced concepts.
Negative Exponents
Negative exponents are a mathematical inverse of positive exponents. Python allows you to handle negative exponents seamlessly.
Fractional Exponents
Fractional exponents bring a new layer of complexity to exponents. Python accommodates fractional exponentiation.
Complex Exponents
Involving complex numbers in exponentiation opens doors to intricate mathematical analysis. Python supports calculations with complex numbers.
Applications of Exponents in Coding
Exponents have practical applications in coding beyond mathematics.
Efficient Algorithms
Certain algorithms, like exponentiation by squaring, leverage the properties of exponents to optimize calculations.
Cryptography
Cryptography relies on the difficulty of certain mathematical operations, such as factoring large numbers into primes.
Exponents vs. Other Operations
A comparison table highlights how exponents differ from other mathematical operations.
| Operation | Description |
|---|---|
| Addition | Combining numbers |
| Multiplication | Repeated addition |
| Exponentiation | Repeated multiplication |
| Division | Sharing a quantity equally |
| Root Extraction | Finding a value that, when raised, yields the original |
Coding Exponents in Python
Let’s dive into practical examples of coding exponents in Python.
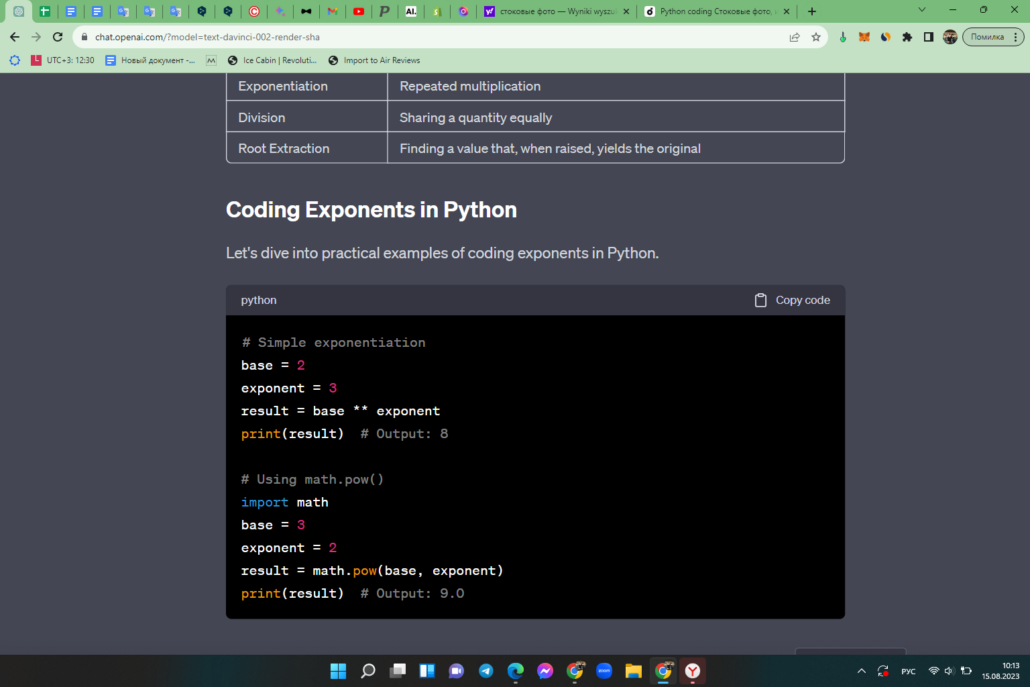
Exponents in Scientific Notation
Scientific notation is a way to represent very large or very small numbers using exponents. In Python, you can easily work with scientific notation to handle these numbers effectively.
Expressing Numbers in Scientific Notation
Scientific notation involves representing numbers as a product of a decimal number between 1 and 10 and a power of 10. For example, 6.02 x 10^23 can be expressed as 6.02e23 in Python.
Using Scientific Notation in Calculations
Scientific notation simplifies arithmetic with large and small numbers. Python automatically handles the arithmetic involving scientific notation.

Exponents and Performance Optimization
Understanding exponents can lead to performance optimization in your Python code, especially in repetitive calculations.
Exponentiation by Squaring
Exponentiation by squaring is an efficient algorithm for calculating large powers of a number. It reduces the number of multiplications required.
Time Complexity Analysis
Understanding the time complexity of exponentiation algorithms helps you choose the most efficient approach for your specific use case.
Exponents and Plotting
Visualization is a powerful tool, and you can use Python libraries to create graphs and plots involving exponential functions.
Using Matplotlib for Exponential Plots
Matplotlib, a popular data visualization library, lets you plot exponential functions and explore their behavior visually.
Analyzing Exponential Growth
Create insightful graphs that depict exponential growth patterns, helping you analyze data trends effectively.
Limitations and Floating-Point Precision
While Python offers remarkable flexibility, it’s important to be aware of potential pitfalls when working with large or small exponents.
Floating-Point Precision Issues
Python’s floating-point arithmetic might introduce small errors when dealing with extremely large or small numbers.
Mitigating Precision Problems
To address precision problems, consider using libraries like decimal that provide arbitrary precision arithmetic.
Conclusion
Exponents are a cornerstone of mathematics and programming, and Python’s capabilities make working with them a breeze. Whether you’re performing complex calculations or optimizing algorithms, mastering exponents will undoubtedly enhance your programming prowess.
FAQs
Exponents in Python are a way to represent repeated multiplication of a number by itself.
Use the ** operator for basic calculations or the math.pow() function for more complex exponentiation.
Absolutely. Python provides seamless support for negative exponents.
Exponents find applications in fields like finance, data science, cryptography, and more.
Exponents represent repeated multiplication, while addition, multiplication, division, and root extraction serve different purposes.

