When it comes to performing mathematical operations in programming, Python stands out for its flexibility and ease of use. One common task is multiplying integers with floating-point numbers. In this guide, we’ll delve into the intricacies of this operation, exploring various methods, best practices, and potential pitfalls.
The Basics of Integer-Floating Point Multiplication
Multiplying integers with floating-point numbers involves combining whole numbers and fractional parts. Python offers intuitive ways to achieve this, ensuring accuracy and precision in calculations. Let’s dive into some fundamental methods.
Method 1: Using the * Operator
The simplest way to multiply integers and floating-point numbers is by using the multiplication operator (*). For instance:
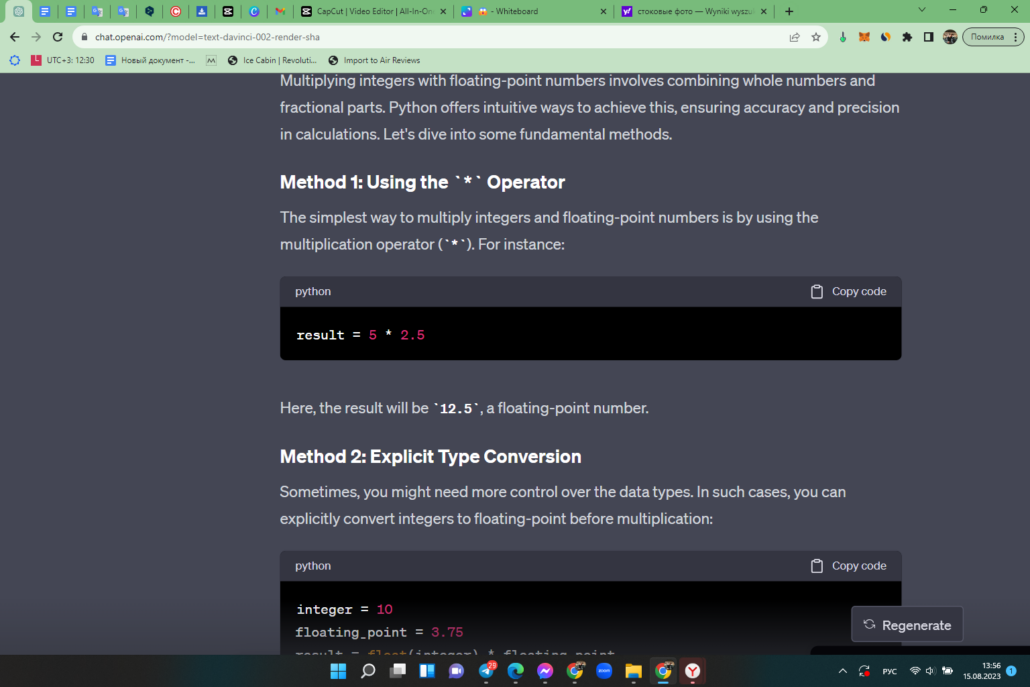
Here, the result will be 12.5, a floating-point number.
Method 2: Explicit Type Conversion
Sometimes, you might need more control over the data types. In such cases, you can explicitly convert integers to floating-point before multiplication:
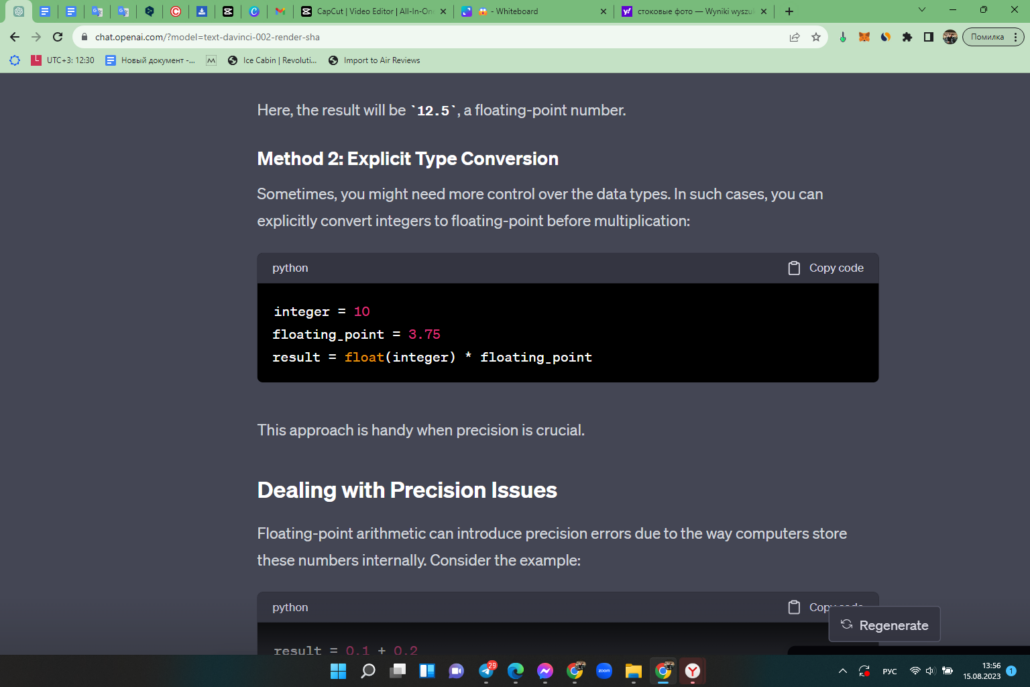
This approach is handy when precision is crucial.
Dealing with Precision Issues
Floating-point arithmetic can introduce precision errors due to the way computers store these numbers internally. Consider the example:
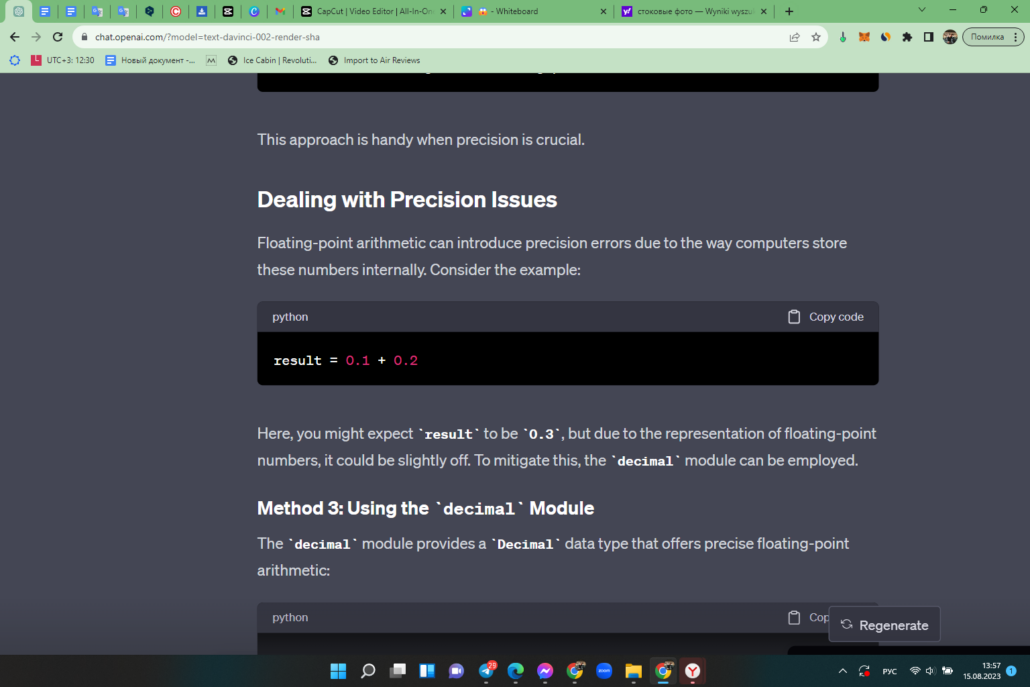
Here, you might expect result to be 0.3, but due to the representation of floating-point numbers, it could be slightly off. To mitigate this, the decimal module can be employed.
Method 3: Using the decimal Module
The decimal module provides a Decimal data type that offers precise floating-point arithmetic:
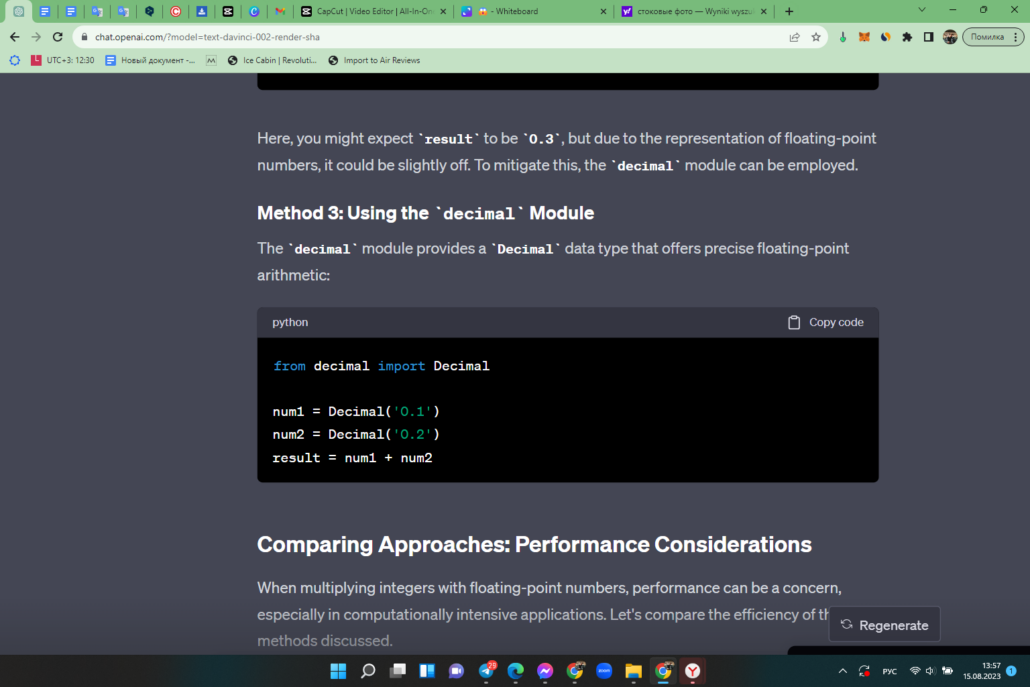
Comparing Approaches: Performance Considerations
When multiplying integers with floating-point numbers, performance can be a concern, especially in computationally intensive applications. Let’s compare the efficiency of the methods discussed.
| Method | Performance | Use Case |
|---|---|---|
| * Operator | Fastest | General-purpose calculations |
| Explicit Conversion | Moderate | Control over data types |
| decimal Module | Slower, precise calculations | Critical precision requirements |
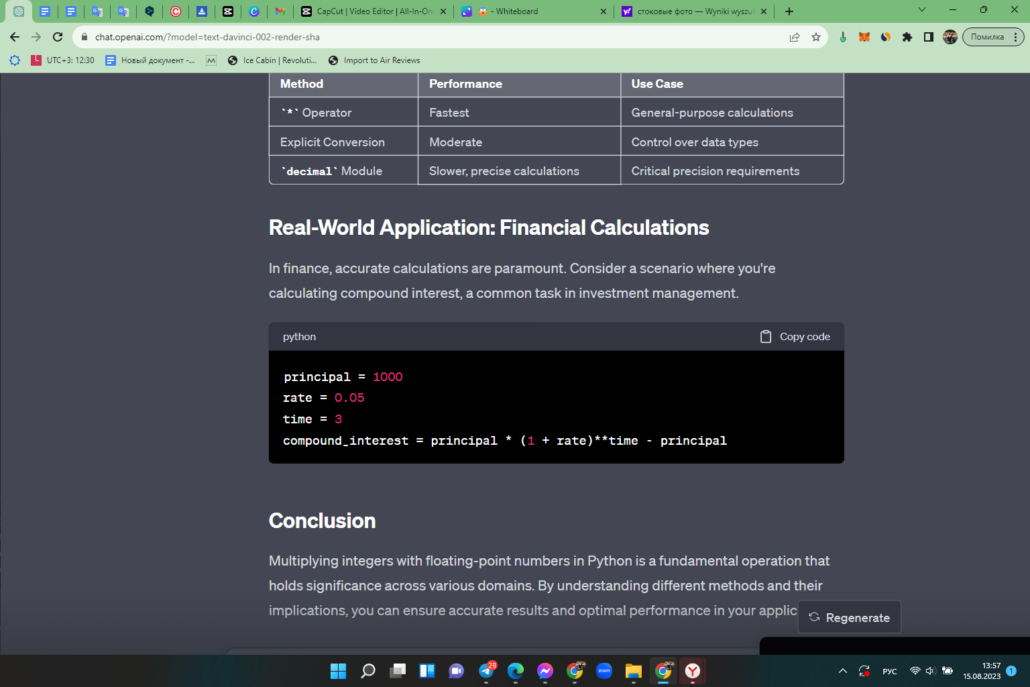
Real-World Application: Financial Calculations
In finance, accurate calculations are paramount. Consider a scenario where you’re calculating compound interest, a common task in investment management.
Advanced Techniques for Improved Accuracy
While the basic methods covered earlier are suitable for many scenarios, more advanced techniques can enhance accuracy and handle complex cases.
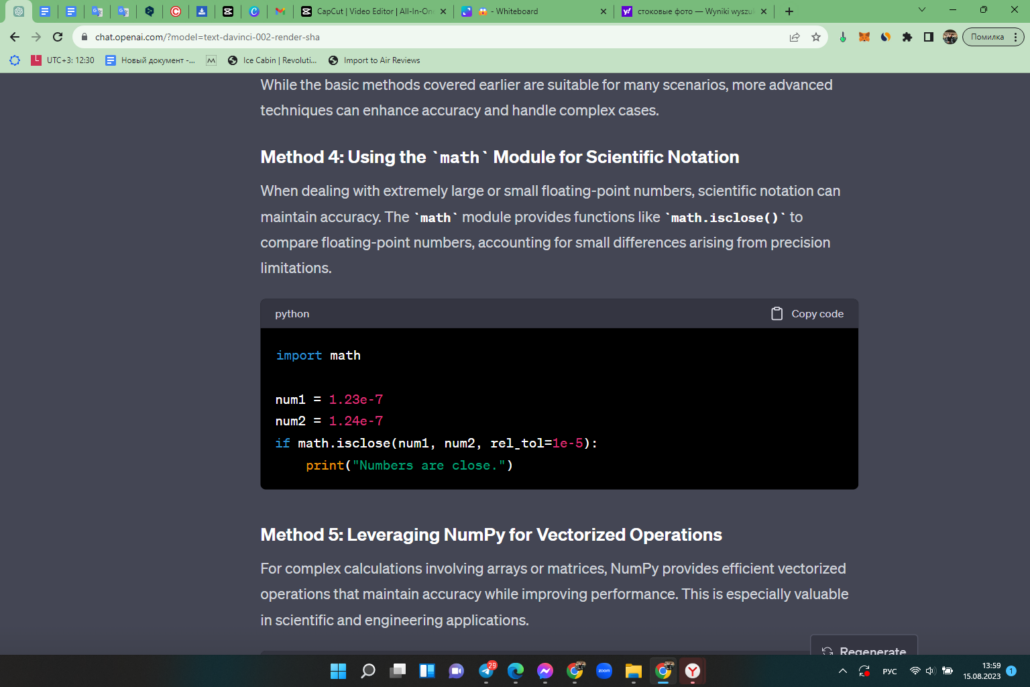
Method 4: Using the math Module for Scientific Notation
When dealing with extremely large or small floating-point numbers, scientific notation can maintain accuracy. The math module provides functions like math.isclose() to compare floating-point numbers, accounting for small differences arising from precision limitations.
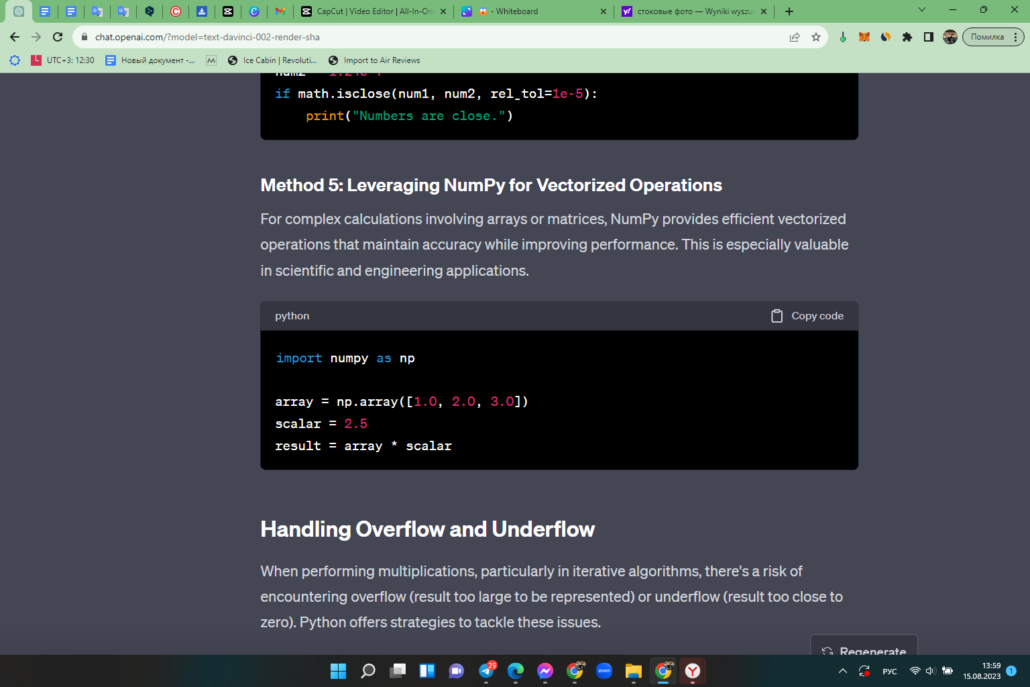
Method 5: Leveraging NumPy for Vectorized Operations
For complex calculations involving arrays or matrices, NumPy provides efficient vectorized operations that maintain accuracy while improving performance. This is especially valuable in scientific and engineering applications.
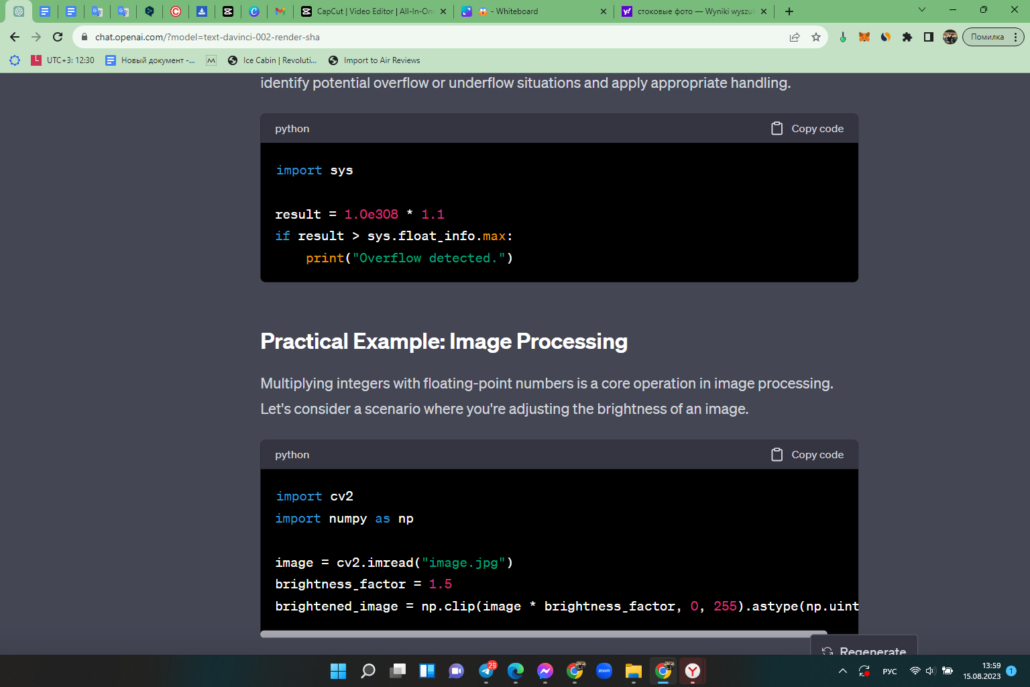
Handling Overflow and Underflow
When performing multiplications, particularly in iterative algorithms, there’s a risk of encountering overflow (result too large to be represented) or underflow (result too close to zero). Python offers strategies to tackle these issues.
Method 6: Using the sys.float_info Constants
The sys.float_info constants provide information about the limits of floating-point representation in Python. By comparing calculated values with these constants, you can identify potential overflow or underflow situations and apply appropriate handling.
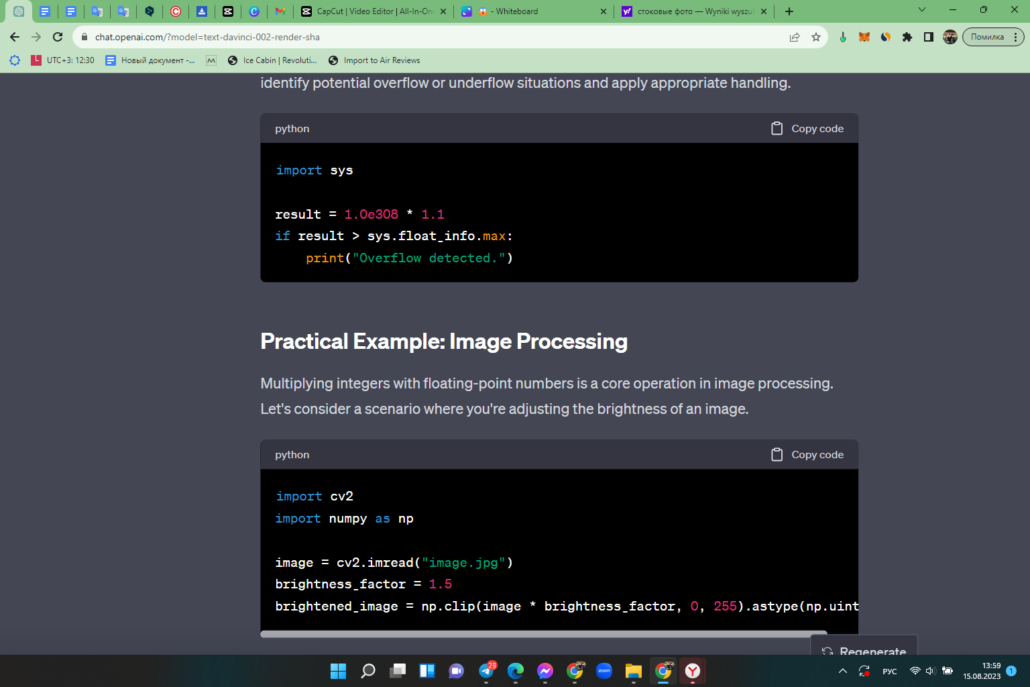
Practical Example: Image Processing
Multiplying integers with floating-point numbers is a core operation in image processing. Let’s consider a scenario where you’re adjusting the brightness of an image.
Conclusion
Multiplying integers with floating-point numbers in Python is a fundamental operation that holds significance across various domains. By understanding different methods and their implications, you can ensure accurate results and optimal performance in your applications.

FAQs
Yes, Python supports operator overloading, allowing you to multiply different data types, including integers and floating-point numbers.
Precision errors arise due to the limitations of representing infinitely many real numbers in a finite amount of memory.
No, the decimal module is mainly required when precision is critical, such as in financial calculations.
Yes, libraries like NumPy offer optimized functions for complex arithmetic operations, including multiplication.
For cross-platform consistency, consider using libraries like numpy or mpmath, which provide more control over floating-point operations.

